Table of contents
分析
明明这题第一个 tag 就是网络瘤流,却没有一篇网络流的题解 qwq。
首先是染色,确定每对曾经跳过舞的学生的性别。
第一个坑,数据不保证无环,所以要这么写:
void color(int x, int c) {
col[x] = c;
vis[x] = true;
for (int i = head[x]; i; i = node[i].nxt) {
int v = node[i].v;
if (vis[v]) { // 如果你按照 v == f 写就会收获 MLE 若干
continue;
}
color(v, c ^ 1);
}
}
有人或许不理解怎么出现环,这里给出一组数据:
5 4
0 1
1 2
2 3
3 0
第二个坑,数据不保证每组前面一定是同种性别。于是你直接建模会收获 40 pts 的好成绩。
我的做法可能有点复杂,供参考。
auto* c = new Color();
for (int i = 1; i <= m; i++) {
int x = read<int>(), y = read<int>();
x++, y++;
c->create(x, y);
c->create(y, x);
c->fm[i] = x;
c->to[i] = y;
}
for (int i = 1; i <= n; i++) {
if (!c->vis[i]) { // 数据不保证联通
c->color(i, 0);
}
}
auto* flow = new Flow(n + 20, s, t);
for (int i = 1; i <= m; i++) {
int x = c->fm[i], y = c->to[i];
if (c->col[x]) {
std::swap(x, y); // 前面的同学颜色不对,交换两位同学
}
flow->create(x, y, 1);
flow->create(y, x, 0);
}
最后注意数据并不保证图的联通,染色的时候不能只跑一遍。
建模
众所周知,网络流主要考建模。
这道题的建模不算很复杂,具体的分析可以看其他题解。
求最大独立集不好求,所以我们求最大匹配,转换为网络流上的最大流。输出答案的时候再拿总点数减一下就好了。
- 不妨假设 的性别为 , 的性别为 。
- 建立容量为 的一条边 。
- 建立超级源点 ,超级汇点 。
- 对于每一个 建立容量为 的一条边 。
- 对于每一个 建立容量为 的一条边 。
就好了啊 qwq。最后流向 的最大流就是二分图上的最大匹配。
还是不太理解的话可以看一下图:
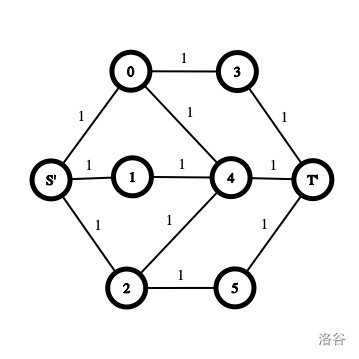
完整代码
Show code
#include <algorithm>
#include <cstdio>
#include <iostream>
class Flow {
private:
const static int MAX_N = 500050;
protected:
struct Node {
int v;
int nxt;
long long w;
} node[MAX_N];
int head[MAX_N], dep[MAX_N], q[MAX_N];
int cnt = 1, n, s, t;
long long ans;
bool bfs() {
std::fill(dep, dep + n + 10, 0);
int l, r;
l = r = 1;
q[l] = s;
dep[s] = 1;
while (l <= r) {
int u = q[l++];
for (int i = head[u]; i; i = node[i].nxt) {
if (node[i].w and !dep[node[i].v]) {
dep[node[i].v] = dep[u] + 1;
q[++r] = node[i].v;
}
}
}
return dep[t];
}
long long dfs(int x, long long flow) {
if (x == t) {
return flow;
}
long long tot = 0;
for (int i = head[x]; i and flow; i = node[i].nxt) {
int y = node[i].v;
if (node[i].w and dep[y] == dep[x] + 1) {
long long res = dfs(y, std::min(node[i].w, flow));
node[i].w -= res;
node[i ^ 1].w += res;
flow -= res;
tot += res;
}
}
if (tot == 0) {
dep[x] = 0;
}
return tot;
}
public:
Flow(int n, int s, int t) {
this->n = n;
this->s = s;
this->t = t;
}
Flow(int n) { this->n = n; }
~Flow() = default;
void create(int u, int v, long long w) {
node[++cnt].v = v;
node[cnt].w = w;
node[cnt].nxt = head[u];
head[u] = cnt;
}
long long dinic() {
while (bfs()) {
ans += dfs(s, 0x7fffffffffffffff);
}
return ans;
}
void set_st(int s, int t) {
this->s = s;
this->t = t;
}
void clear() {
std::fill(node, node + cnt + 10, (Node){0, 0, 0});
std::fill(head, head + cnt + 10, 0);
std::fill(q, q + n + 10, 0);
n = s = t = 0;
cnt = 1;
ans = 0;
}
};
class Color {
private:
const static int MAX_N = 500050;
public:
Color() = default;
~Color() = default;
struct Node {
int v;
int nxt;
} node[MAX_N];
int head[MAX_N];
int cnt;
int fm[MAX_N], to[MAX_N];
int col[MAX_N];
bool vis[MAX_N];
void create(int u, int v) {
node[++cnt].v = v;
node[cnt].nxt = head[u];
head[u] = cnt;
}
void color(int x, int c) {
col[x] = c;
vis[x] = true;
for (int i = head[x]; i; i = node[i].nxt) {
int v = node[i].v;
if (vis[v]) {
continue;
}
color(v, c ^ 1);
}
}
};
template <typename T>
T read();
int main() {
std::ios::sync_with_stdio(false);
int n = read<int>(), m = read<int>();
int s = n + 10, t = n + 11;
auto* c = new Color();
for (int i = 1; i <= m; i++) {
int x = read<int>(), y = read<int>();
x++, y++;
c->create(x, y);
c->create(y, x);
c->fm[i] = x;
c->to[i] = y;
}
for (int i = 1; i <= n; i++) {
if (!c->vis[i]) {
c->color(i, 0);
}
}
auto* flow = new Flow(n + 20, s, t);
for (int i = 1; i <= m; i++) {
int x = c->fm[i], y = c->to[i];
if (c->col[x]) {
std::swap(x, y);
}
flow->create(x, y, 1);
flow->create(y, x, 0);
}
for (int i = 1; i <= n; i++) {
if (c->col[i]) {
flow->create(i, t, 1);
flow->create(t, i, 0);
} else {
flow->create(s, i, 1);
flow->create(i, s, 0);
}
}
int f = flow->dinic();
std::cout << n - f << '\n';
return 0;
}
template <typename T>
T read() {
T x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-') f = -1;
ch = getchar();
}
while (isdigit(ch)) {
x = x * 10 + ch - 48;
ch = getchar();
}
return x * f;
}